La posición relativa de dos rectas es un tema fundamental en el estudio de la geometría. Permite determinar si las rectas son paralelas, coincidentes, secantes o se cruzan en algún punto. Este conocimiento es esencial en diversas áreas, como la geometría analítica, la física y la ingeniería, ya que permite resolver problemas en los que se requiere conocer la intersección de dos rectas.
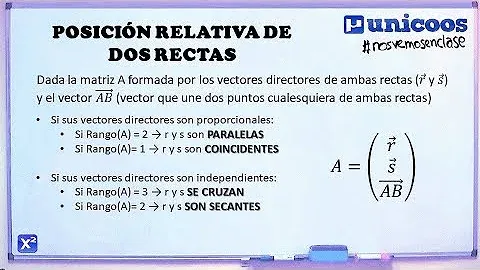
Existen diversas formas de determinar la posición relativa de dos rectas. Una de ellas es analizando los vectores directores de las rectas. Si estos vectores son proporcionales, las rectas pueden ser paralelas o coincidentes. Para distinguir entre estas dos opciones, se debe comprobar si un punto de una recta cumple con la ecuación de la otra recta. Si el punto cumple con la ecuación, las dos rectas son coincidentes. Si no cumple, son paralelas. Por otro lado, si los vectores no son proporcionales, las rectas pueden ser secantes o se cruzan en algún punto. En este caso, se debe resolver un determinante 3×3 formado por el vector director y un punto de cada recta. Si el determinante es igual a cero, las dos rectas se cortan en un punto y son secantes, mientras que si es diferente de cero, se cruzan en algún punto en el plano.
Otra forma de determinar la posición relativa de dos rectas es calculando los rangos de dos matrices concretas. Si el rango es 1, las rectas son secantes y se cortan en un punto. Si el rango es 2, las rectas son paralelas y no se cortan en ningún punto. Si el rango es 3, las rectas son coincidentes y todos sus puntos son comunes. Esta forma de análisis puede resultar útil en situaciones en las que se requiere una solución rápida y precisa.
¿Qué es la posición relativa de dos rectas?

La posición relativa de dos rectas se refiere a la relación que existe entre ellas en el espacio tridimensional (R3). En geometría analítica, se pueden identificar cuatro posibles posiciones relativas entre dos rectas: rectas coincidentes, rectas paralelas, rectas secantes y rectas que se cruzan.
Las rectas coincidentes son aquellas que tienen la misma dirección y todos sus puntos son comunes. Esto implica que ambos segmentos son iguales y se encuentran en la misma ubicación en el espacio.
Las rectas paralelas son aquellas que tienen la misma dirección pero no tienen ningún punto en común. Estas rectas siempre están a la misma distancia entre sí y nunca se intersectan.
Las rectas secantes son aquellas que tienen direcciones diferentes pero se tocan en un punto. Esto significa que comparten un único punto de intersección en el espacio.
Las rectas que se cruzan son aquellas que tienen direcciones diferentes y no se intersectan en ningún punto. Por lo tanto, no están en el mismo plano y se cruzan en alguna parte del espacio.
Para determinar la posición relativa de dos rectas, se pueden utilizar diferentes métodos. Uno de ellos es verificar si los vectores directores de las rectas son proporcionales. Si lo son, las rectas pueden ser paralelas o coincidentes. En este caso, se debe comprobar si un punto de una recta cumple con la ecuación de la otra recta. Si es así, las rectas son coincidentes; de lo contrario, son paralelas.
Si los vectores directores no son proporcionales, las rectas pueden ser secantes o que se cruzan. En este caso, se puede resolver un determinante formado por el vector director y un punto de cada recta. Si el determinante es igual a cero, las rectas son secantes; si es diferente de cero, se cruzan.
Otra forma de determinar la posición relativa de dos rectas es calculando los rangos de dos matrices concretas. Este método es útil cuando las rectas están en forma de ecuación implícita o general.
¿Cómo se obtiene la posición relativa de dos rectas?
Para obtener la posición relativa de dos rectas, es necesario seguir un proceso que incluye varios pasos. Este proceso se basa en las propiedades de las rectas y su relación con las ecuaciones implícitas que las representan.
1. Pasar las ecuaciones continuas a ecuaciones implícitas
El primer paso es convertir las ecuaciones continuas de las rectas en ecuaciones implícitas. Esto significa que se deben reordenar los términos para que todos los términos con las variables queden de un lado de la igualdad y los términos constantes del otro lado.
Por ejemplo, si se tienen las rectas y = 2x + 3 y y = -3x + 5, se pueden reescribir como 2x – y = -3 y 3x + y = 5 respectivamente.
2. Hallar el rango de la matriz de los coeficientes
Una vez que se tienen las ecuaciones implícitas, se deben representar en forma de matriz y encontrar su matriz de coeficientes. Esta matriz se obtiene eliminando la columna correspondiente a los términos constantes de la matriz ampliada.
Por ejemplo, si se tienen las ecuaciones del paso anterior, su matriz de coeficientes sería [2, -1] y [3, 1] respectivamente.
3. Determinar el rango de la matriz ampliada
Ahora se debe encontrar la matriz ampliada, que se obtiene agregando una columna extra a la matriz de coeficientes con los términos constantes. Luego se debe encontrar su rango, que es la cantidad de columnas o filas independientes que tiene la matriz.
Utilizando el ejemplo anterior, la matriz ampliada sería [2, -1, -3] y [3, 1, 5] respectivamente. Al encontrar su rango, se obtiene que ambos tienen un rango de 2.
4. Comparar los rangos obtenidos
Finalmente, se deben comparar los rangos obtenidos en el paso anterior. Si los rangos son iguales, significa que las ecuaciones representan rectas paralelas. Si los rangos son distintos, significa que las ecuaciones representan rectas que se cruzan en un punto.
En el primer ejemplo proporcionado, ambas matrices tienen un rango de 2, por lo que se concluye que las rectas son paralelas. En el segundo ejemplo, las matrices tienen distintos rangos, por lo que se determina que las rectas se cruzan en algún punto.
Este proceso es útil para obtener la posición relativa de dos rectas en cualquier situación, ya que se basa en las propiedades generales de las ecuaciones de rectas. Siguiendo estos pasos y comparando los rangos de las matrices, se puede determinar si las rectas son paralelas, intersectan en un punto o no tienen una intersección.
¿Qué es posición relativa en geometría?
La posición relativa en geometría se refiere a las diferentes formas en las que dos rectas pueden interactuar en el espacio tridimensional. En este contexto, nos referimos a cómo las rectas se relacionan entre sí en términos de su dirección, puntos en común y si se intersectan o no. En geometría analítica, existen cuatro posibles posiciones relativas entre dos rectas: coincidentes, paralelas, secantes o que se cruzan.
- Dos rectas son paralelas si tienen la misma dirección pero no tienen ningún punto en común. Además, siempre están a la misma distancia entre sí.
- Dos rectas son coincidentes si tienen la misma dirección y todos sus puntos son comunes.
- Dos rectas son secantes si tienen direcciones diferentes pero se tocan en un punto.
- Dos rectas son que se cruzan si tienen direcciones diferentes y no se intersecan en ningún punto. Por lo tanto, no están en el mismo plano.
Para determinar la posición relativa de dos rectas, se pueden utilizar dos métodos dependiendo de cómo estén expresadas las ecuaciones de las rectas.
1. Si las rectas están en forma de ecuación vectorial, paramétrica o continua, se puede utilizar un punto y un vector de cada recta para calcular su posición relativa.
2. Si las rectas están definidas en forma de ecuaciones implícitas o generales, se puede calcular el rango de dos matrices para determinar su posición relativa.
¿Cuáles son las diferentes posiciones relativas de dos rectas?
Existen diferentes posiciones relativas que pueden tener dos rectas en el espacio tridimensional (en R3). Estas posiciones se clasifican en: rectas coincidentes, rectas paralelas, rectas secantes y rectas que se cruzan. Cada una de estas posiciones tiene sus propias características y condiciones.
- Rectas coincidentes: Dos rectas son coincidentes cuando tienen la misma dirección y todos sus puntos son comunes. Esto significa que las dos rectas son idénticas y se superponen completamente.
- Rectas paralelas: Dos rectas son paralelas cuando tienen la misma dirección pero no tienen ningún punto en común. Además, siempre están a una misma distancia entre sí. Esto indica que las dos rectas son paralelas entre sí y no se cruzan en ningún punto.
- Rectas secantes: Dos rectas secantes tienen diferente dirección y se tocan en un punto. Aunque no comparten todos sus puntos, sí tienen un punto de intersección en común.
- Rectas que se cruzan: Dos rectas que se cruzan tienen distinta dirección y no se intersecan en ningún punto. Estas rectas no están en el mismo plano y se cortan en un punto.
Para determinar la posición relativa de dos rectas, se pueden utilizar diferentes métodos. Uno de ellos es verificar si los vectores directores de las rectas son proporcionales. Si lo son, las rectas pueden ser paralelas o coincidentes. En este caso, se debe comprobar si un punto de una recta cumple con la ecuación de la otra recta para determinar si son coincidentes.
Si los vectores directores no son proporcionales, las rectas pueden ser secantes o que se cruzan. En este caso, se puede resolver un determinante 3×3 formado por el vector director y un punto de cada recta. Si el determinante es igual a cero, las rectas se cortan en un punto (son secantes). Si el determinante es diferente de cero, las rectas se cruzan.
Otro método para determinar la posición relativa de dos rectas es calcular los rangos de dos matrices concretas. Este método es útil cuando las rectas están en forma de ecuación implícita (o general). Dependiendo de los rangos obtenidos, se puede determinar si las rectas son paralelas, coincidentes, secantes o que se cruzan.
¿Qué es la posición relativa de una recta y un plano?

La posición relativa de una recta y un plano se refiere a cómo interactúan entre sí en el espacio tridimensional. En términos de geometría analítica, hay cuatro posiciones relativas principales en las que una recta y un plano pueden encontrarse: paralela, perpendicular, contenida y oblicua.
En el caso de una recta paralela a un plano, esto significa que la recta y el plano no tienen ningún punto en común y siempre están a la misma distancia entre sí. Por ejemplo, si dibujamos una línea recta en el aire sobre una mesa, esta línea no tocará la superficie de la mesa en ningún punto.
En el caso de una recta perpendicular a un plano, la recta y el plano se intersectan en un solo punto. Imagina una línea recta dibujada verticalmente sobre una hoja de papel. La línea atravesará la superficie del papel en un solo punto de intersección.
Si la recta está contenida en el plano, esto significa que todos los puntos de la recta también pertenecen al plano. Podemos imaginar una línea recta dibujada directamente sobre la superficie de un escritorio. Cada punto de la línea coincide con un punto del plano.
Finalmente, si la recta y el plano son oblicuos, se intersectan en más de un punto, pero no están contenidos uno en el otro. Por ejemplo, si dibujamos una línea inclinada en relación a una hoja de papel, la línea cortará la superficie en varios puntos, pero la línea no estará completamente dentro o fuera del plano.
¿Cómo se clasifican las rectas según su posición?
La clasificación de las rectas según su posición en el espacio tridimensional se puede dividir en cuatro categorías: rectas coincidentes, rectas paralelas, rectas secantes y rectas que se cruzan. Esta clasificación se basa en la relación que tienen las rectas entre sí y la forma en que se intersectan en el espacio.
Por un lado, dos rectas son paralelas si tienen la misma dirección pero no tienen ningún punto en común. En otras palabras, no se intersecan y siempre mantienen la misma distancia entre sí. Esto significa que son infinitas rectas que no se cruzan en ningún punto. Un ejemplo común de rectas paralelas es el caso de dos rieles de tren que se extienden hacia el horizonte.
Por otro lado, dos rectas son coincidentes si tienen la misma dirección y todos sus puntos son comunes. Es decir, son rectas que ocupan exactamente el mismo espacio y tienen infinitos puntos en común. Un ejemplo de rectas coincidentes es la línea del ecuador y el meridiano de Greenwich, ya que ambos comparten los mismos puntos y dirección en el globo terráqueo.
Para determinar la posición relativa de dos rectas en el espacio tridimensional, existen diferentes métodos que se pueden utilizar. Uno de ellos es verificar si los vectores directores de las rectas son proporcionales. Si esto es cierto, entonces las rectas pueden ser paralelas o coincidentes. En este caso, se debe comprobar si un punto de una recta cumple con la ecuación de la otra recta para determinar si son coincidentes o paralelas.
¿Cómo se aplica la posición relativa de dos rectas en la vida cotidiana?
La posición relativa de dos rectas es una herramienta fundamental en diferentes áreas de la vida cotidiana. En el campo de la geometría analítica, comprender las cuatro posibles posiciones entre dos rectas puede ser útil para resolver problemas de diseño y construcción, así como para realizar mediciones precisas en diferentes estructuras. Además, esta herramienta también tiene una gran importancia en la física, ya que permite determinar la dirección y el punto de intersección de diferentes objetos en movimiento, lo cual es fundamental en el estudio de la cinemática y dinámica de los cuerpos.
Un ejemplo claro de la aplicación de la posición relativa de dos rectas es en la construcción de carreteras y autovías. En este tipo de proyectos, es fundamental asegurar que las líneas de los carriles sean paralelas entre sí para garantizar una circulación segura y fluida. Si estas líneas no tuvieran la misma dirección, podrían producirse accidentes y problemas en la circulación de vehículos.
Otra aplicación común de la posición relativa de dos rectas se encuentra en la navegación marítima y aérea. En estos casos, es necesario tener en cuenta la posición de diferentes líneas de guía para determinar la dirección y la velocidad de un objeto en movimiento. Los aviones y barcos deben seguir una ruta específica y deben tener en cuenta la posición de otras líneas de referencia, como la línea del horizonte o la línea del viento, para lograr una navegación segura y precisa.
Ejemplos de la posición relativa de dos rectas
Para entender mejor cómo se determina la posición relativa de dos rectas en el espacio, podemos usar ejemplos cotidianos. Por ejemplo, pensemos en dos carriles de una carretera que son paralelos y nunca se intersectan entre sí. Además, mantienen una distancia constante uno del otro a lo largo de su recorrido. Esta sería una representación de dos rectas paralelas en el espacio.
Otro ejemplo común podrían ser dos líneas de tendido eléctrico que corren cerca una de la otra sin tocarse. Aunque estas líneas pueden tener diferentes alturas en algunos puntos, nunca se intersectan, lo que las hace rectas secantes. En este caso, cada línea tendría una dirección diferente pero en algún punto se tocarían.
En el ámbito de la geometría, se pueden encontrar otros ejemplos de la posición relativa de dos rectas. Por ejemplo, en un plano cartesiano, dos rectas coincidentes serían dos líneas que tienen la misma pendiente y se superponen, es decir, comparten todos sus puntos. Mientras que dos rectas paralelas en el mismo plano tendrían la misma pendiente pero nunca se tocarían entre sí.
Asimismo, en geometría analítica se utilizan ciertos métodos para determinar la posición relativa de dos rectas. El método del punto y el vector es uno de ellos, en el que se comparan las coordenadas de un punto y un vector de cada recta para determinar si los vectores son proporcionales o no. Dependiendo de esta relación, se puede determinar si las rectas son paralelas, coincidentes, secantes o que se cruzan en algún punto.
Errores comunes y recomendaciones en el estudio de la posición relativa de dos rectas
Existen diferentes conceptos y posiciones relativas entre dos rectas en un espacio tridimensional (en R3), por lo que es común cometer errores al estudiar su posición. Uno de los errores más comunes es no considerar las diferentes posiciones relativas posibles: coincidentes, paralelas, secantes o que se cruzan. Es importante tener en cuenta estas posiciones para realizar correctamente los cálculos y determinar la posición relativa de las rectas.
Otro error frecuente es no tener en cuenta que las rectas cruzadas no están en el mismo plano. Dos rectas que se cruzan tienen distinta dirección y nunca se interceptan en un punto. Por lo tanto, es crucial recordar que dos rectas cruzadas no pueden estar en el mismo plano y no se debe asumir lo contrario al realizar cálculos o dibujar gráficas.
Para evitar estos errores comunes, es recomendable repasar los conceptos básicos de la geometría analítica y tener en mente todas las posibles posiciones relativas entre dos rectas. También es crucial hacer un esquema o una representación visual de las rectas en un plano cartesiano para ayudar a visualizar su posición relativa y evitar confusiones. Además, se recomienda siempre verificar los resultados obtenidos a través de diferentes métodos, como resolver sistemas de ecuaciones o utilizar fórmulas específicas para cada posición relativa.